[TP-Link TL-R483G Industrial router] Config.bin file Decrypted

Hi Folks,

 

today I'm gonna take a quick look to the TP-Link TL-R483G sold in China.
I've got a chance to have a firmware and config file on Github so I decided to dig into it.

Once unpacked the firmware (standard uboot image), the references on encryption/"save configs" brings me on firmware_backuprestore.lua script file.

firmware_backuprestore.lua

by going straight to the executable, I noticied that the config encrypted file has 0x10 bytes of signature (by reading the typical initialize variables can be md5, not sure anyway).
So, the encrypted data starts from 0x10 to the EOF

from the elf opened with Ghidra, I've been able to figure out which encryption it was applied and to read the key by ease:

It is a des-ecb encryption with key 0x478DA50FF9E3D2CB and no padding.

By putting the things togheter, with the help of the amazing CyberChef tool I've got as resoult a decrypted data which starts with 0x1f8b: the GZIP magic bytes! 🥳

 CyberChef recipe

Anyway, the GZIP file conains a tar, so the decrypted data is basically a config.tar.gz file which contains the entire /tmp/cfg_save folder.

 Cheers,
RE-Solver

[ CVE-2022-40602 ] ZyXEL LTE3301-M209 - "Backdoor" credentials

Hi Folks,

as a continuation from the previous post, we're going to take a look at ZyXEL LTE3301-M209.

[!] Togheter with Zyxel PSIRT, we decided not to reveal the credentials. In addition, due to the impact it may have, some steps are skipped.

 

The telnet "backdoor" is not limited to the D-Link DWR-921 and seems to be present on the ZyXEL LTE3301-M209 as well. 

FW version: 20191202 V1.00(ABLG.4)C0 

MD5:8A2C093431456BFDC8D3DD0403EC1632

Same speech, let's go straight to the commander elf, as seen in the previous post:

commander elf from ZyXEL fw

 
same amit* functions, same producer means same backdoor?! Not really.

In the first case, since having the D-Link phisically, I had a chance by rdcsman tool to read the password from the device. I now have no phisical access to the device and I have to dig the password out from the config.

The firmware is basically a merge of 3 sections, the LZMA section is the kernel, at  0x148CD6 the root-fs and at  0x90BD36 the www content.

Inside the last Squashfs there is a [censored] file which is contains at 0x10 the Zlib magic bytes.

To unpack the file you can use openssl or zlib-flate in unix or alternatively transform the zlib into a gzip file in windows and make it readable by 7zip.

Going brutally down by strings there is no one good telnet password however....

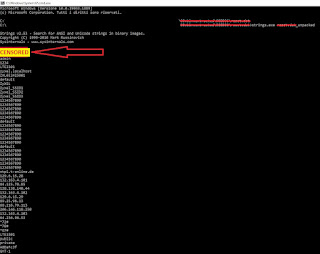WebUI Credentials

An interesting sequence appeared: username / WebUIFakePassword .

By looking at telnet creds I've actually landed on something which looks like a backdoor in the webUI!!

[few steps are hidden]

Same as before and unpack the config.dat is going to contain the telnet login password: "TelnetFakePassword"

Let's put things togheter:
On ZyXEL LTE3301 we have two ways to own the device:

1) webUI credentials --> username / WebUIFakePassword

2) telnet credentials  --> root / TelnetFakePassword

An additional note: from what i see, telnet password is not included in the reset.dat so, if rewritten, it may remain permanently modified regardless of reset.

Upgrade your device with the latest firmware ASAP! 

History:
12 Sep 2022: Vulnerability reported to ZyXEL

13 Sep 2022: ZyXEL asks for detail in order to replicate the vulnerability.
13 Sep 2022: Details sent to ZyXEL.

14 Sep 2022: ZyXEL confirm that the issues only affect the LTE3301-M209 model. They're working to the vendor to fix it. They asks to keep information confidential until patch has released.
17 Sep 2022: Waiting for the patch.

19 Oct 2022: The issue is now tracked by CVE-2022-40602
22 Nov 2022: ZyXEL's security bullettin published. Firmware fix has been released. 

24 Dec 2022 Hopefully users has now updated their own devices, It's time to make my blog post public.

Cheers!
RE-Solver

[D-Link DWR-921 | DWR-925 | DWR-118 ] Hardcoded backdoor implemented by vendor

Hi Folks,

I owned a D-Link DWR-921 HW:C3 with OpenWRT, but once no longer in use I decided to put the stock firmware back and as consequence the need to have a console root access. 😁

This device has been probably made by AMIT Enabling Wireless M2M-IoT - amit.com.tw

[!] Due to the impact it may have, credentials are hidden.

The FW image itself is basically standard, except for the squashfs header, which are in a non standard format and the unpack fails, no matter which tool you're gonna use.
By hand-made analysis, a pretty easy header portion swap has restored the structure. *Ask me on comments below or twitter if you wanna know more about that topic.*

My mainly goal was to get a console, telnet or ssh, or whatever.

 

Keep in mind: The /etc/passwd file has the login credentials for root with this encoded password:

root:$1$$N76hdwGfg11g0KdKbtyh21:0:0:root:/root:/bin/ash

 

A quick online search and the corresponding plaintext password is: amittima (the productor name palindromized: Amit Company)
Good to know, but not very useful at the moment, since there is no remote console available.

I started out with the belief that I had to find a controllable variable for a quick code injection, I would not have expected such a blatant backdoor nowdays.
A brief check on rcS to get an idea of how the boot process is structured, and a quick shoot with Ghidra on httpd and commander ELFs.
Among all the strings in httpd, "telnetd -b 0.0.0.0" was the most interesting one.
A picture speaks more than a thousand words.

httpd

 

Yes, a GET request at the url http://ipmodem/atsq.txt cause the system call which starts the telnetd process on all interfaces. Yeah, all interfaces, WAN included. {facepalm}

Telnet service is up and running, but with the root/amittima tuple won't allow us to login.
In a few forums other users wrote they were unable to login as well

Serial console is enable by default on router serial, so I took the advantage with a USB-TTL interface to give a check on the passwd file:

# cat /ram/etc/passwd
root:$1$$taSOMETHINGYOUHAVENOTTOKNOWJ41:0:0:root:/root:/bin/ash
nobody:$1$$qRPK7m23GJusamGpoGLby/:99:99:nobody:/var/usb:/sbin/nologin
ftp:$1$$qRPK7m23GJusamGpoGLby/:14:50:FTP USER:/var/usb:/sbin/nologin 

The password must be overwritten by some process during the boot.
The /sbin/commander ELF is the only which contains "/etc/passwd" in the strings and has a file write attribute to that file.

commander

Router settings in the flash are managed by csman and the root password is going to be ridden by csman and then encrypted by standard crypt(...) call.
Empty salt "$1$" confirmed already in the passwd file.
rdcsman is the console application included into the firmware to read variables into the config mtd partition structured in a way which I want to ignore.

 #  rdcsman 0x1 str
DLinkPassword

Put things togheter:

1) turn on the telnet: a GET request to routerip/atsq.txt (a browser is fine)
2) root credentials are: root/DLinkPassword

  And that's it, we're in!

telnet

 

But, wait a sec... what if I search for RT305XL on shodan? I hopfully expect zero results but there are several of them.

Bonus: 

D-Link  DWR-925 telnet access --> root / DLinkPassword2

D-Link  DWR-118 telnet access --> root / DLinkPassword

History:
12 Sep 2022: Vulnerability reported to D-Link

19 Sep 2022: No response, 2nd warning through email sent. 

27 Sep 2022: D-Link has released a security bullettin. But they're not going to fix the backdoor.

Cheers!
RE-Solver

Ho-mobile Data breach series: What if they suffer from a User Enumeration weakness?

Hello Folks, talking about an Italian mobile phone carrier it's time for me to write in Italian. Sorry for that.

Ebbene si, pare proprio che oltre 2.5milioni di clienti abbiano la propria identità in giro per il mondo, come se non bastasse, anche il proprio ICCID.

Posizioniamoci cronologicamente prima del databreach e facciamo uno sforzo d'immaginazione.
Ipotizziamo un attore capace di controllare quale numero di telefono è utente Ho-mobile e di aggiungere a questa informazione quanti e quali numeri di telefono fanno capo ad una singola persona fisica, il tutto con un semplice script in Python.

Un call center qualunque, uno di quelli che se ne infischia delle regole (state pensando: "tutti", vero?!), a questo punto potrebbe offrire pacchetti mirati, cuciti su misura, in ordine alle utenze in possesso da ogni singolo target, inoltre si risparmierebbe un considerevole numero di chiamate, conoscendo in anticipo che ad un certo numero di numeri telefonici, risponderebbe verosimilmente la stessa persona fisica.

Questa sceneggiatura nacque nella mia mente quando scrissi un piccolo script (legittimo) per tenere sotto controllo il traffico e il credito residuo della mia sim.
Laddove qualcuno ne sia interessato: https://pastebin.com/TM1CMx3i

Diamo una sommaria occhiata a come Ho-mobile gestisce il login per il tramite delle loro REST-API: 

In sostanza, il server di ho-mobile, tra le altre informazioni, risponde con un accountId che rappresenta il codice cliente, 'None' se quel numero non appartiene al bacino dei loro clienti.
Ecco qui che l'ipotesi di una ricerca di massa (bulk) fondata sui numeri di cellulare prende forma.

L'accountId è lo stesso per ogni numero di telefono ricercato (personalmente possiedo due numeri di cellulare ho-mobile e con ognuno di esso posso effettuare l'accesso, ed ottengo in risposta un solo,lo stesso, accountId perchè quest'ultimo è l'elemento legato alla password). Con questa informazione si rappresenta una relazione tra numero di telefono e utente "N:1".

I più maliziosi penseranno: "Ma dopo un certo numero di richieste banneranno l'ip, bloccheranno l'account, forzeranno la verifica dell'account o inseriranno un captcha!" 

La risposta è che ciò che so è che persi la password del mio account, e nel provare le varie (tante) che ritenevo possibili per accedere al MIO personale account, nonostante le abbia provate dallo stesso ip in un frangente di tempo minimo, non ho innescato nel loro server nessun tipo di protezione (forse perchè proprio non ne implementano alcuna!?).

Dalle testate giornalistiche leggo che Ho-mobile «non ha evidenze di accessi ai propri sistemi» - di fatto  quindi - non conferma, ma nemmeno smentisce la notizia.

Se hanno strutturato così il loro sistema di login, fosse davvero avvenuto il data breach, seriamente ci dovrebbe stupire?!
 

RE-Solver

Linksys RE6500 - CVE-2020-35713 CVE-2020-35714 CVE-2020-35715 CVE-2020-35716 - Unauthenticated RCE: Full Disclosure

Linksys RE6500 is a pretty new range extender build by Linksys, well, more properly by Belkin. An USA product built just a few thousand km east in the "suicide factory" (the Foxconn factory, China)

My goal was to archive a personal need a telnet access, I never expected to come across such a big security hole holes, more properly because between poorly implemented backdoor ( goform/j78G-DFdg_24Mhw3?password= ) and lousy code, in the end I discovered a few security flaws.

tl;dr

li a0, "RCE"

jmp a0

Index

0 - Encrypted Firmware

1 - Code injection into diagnostic (ping webpage)

2 - Code injection in config file upload

3 - Persistent webui DOS potentially exploitable

4 - Unauthenticated RCE

5 - Extra: Download latest beta firmware for any Linksys products

TP-Link RE200 config.bin decryption and manipulation

A very quick article to share with you how to decrypt the TP-Link RE200 config.bin

In this article we take up the concepts seen in the previous one jumping straight into Ghidra to take a look at the _tddp_UploadFlashData routine in httpd ELF.

The way the config is being uploaded is pretty clear, basically the uploaded file is entirely decrypted, after which the md5 hashing is performed starting from the 0x10 offset until the end of the file. Finally, it verifies whether the first byte 0x10 coincide in this md5.
The encryption has been performed with a DES symmetric-key algorithm (ECB)

Demonstration:

Openssl can reach the goal by using this command:
# openssl enc -d -des-ecb -nopad -K 478DA50BF9E3D2CF -in config.bin > decrypted.bin

alternatively you can use any other application, demonslay335's CryptoTester for example:

 copy and paste the decrypted data into an hxd

Do a manually md5 check by selecting all the bytes from 0x10 to the end of the file.

You can now modify by a text editor the decrypted confing, retrive and or change the admin password, recalculate the new md5, encrypt the whole file back and upload it by the web interface. That's all. :)


Follow me on Twitter


Cheers,
RE-Solver

TP-Link RE200 aka AC750: Unpack, repack, validate image by md5 hashing and upload YOUR OWN version!

This article demonstrates how "easy" may be build a potentially malicious firmware. 
This way should be valid for EVERY TP-Link firmware header version 1 (identified by the very first 4 bytes in the header, in little endian!)

A TP-Link RE200 is a widespread cheap Range Extender.
I love having root shell on my devices, so long story short:
I've started to decrypt RE200 config.bin (which I'll publish soon Edit: here!), to find a vector to inject code and get a root shell.
Unfortunatelly, for this time, the firmware is (not really, but enough) well written so I couldn't see any code injection possibilities from the browser and/or from the nvram config file and (almost) every stack smash chance are avoided by reimplemented TP-Link functions.

Ok, excluding a phisical attack, a custom firmware is the common route (among the same family devices) to get the shell.

Index:
0 - rcS script
1 - firmware header structure - httpd Analysis with Ghidra
2 - firmware customization and squashfs recompression
3 - firmware file reconstruction
  3.1 - Uncompress the image
  3.2 - Modify
  3.3 - Re-Compress the image
  3.4 - Put the things togheter
4 - Firmware mod new hash
5 - Upload and verify

0 - rcS script

Once unpacked the firmware by using binwalk ($ binwalk  -e firmware.bin ) the first thing to take a look at RunControlSingle user script (rcS).

Pretty clear,  TP-Link has commented the telnet row command, disabling the daemon.
In the end we'll see the httpd start command.

1 - firmware header structure - httpd Analysis with Ghidra

Let's start to examinate the firmware header in Ghidra. Our focus lands on upgradeFirmware(void *param_1,uint param_2)

I will try to be as brief as possible. Additional explainations requests in comments are welcome
1- In a similar way we seen in the config.bin [here], the file offset 0x4c contanins the md5 hash signature
2- int variable in 0x94 indicates if our firmware conains bootloader. If yes, the md5 signature uses a different salt.
3- md5_veryfy_digest. No explaination, this works in the same way as in the config.bin. Getting the md5  from the file in a variable, it replaces the same file address readen 0x4c with the 0x10 bytes with the right salt on point 2. It calculates the md5, and compare with the one originally readen.
4- Country code check @ 0x98 len=3chars: in case we'll change the firmware from a different country, we need to restore the same country code the device is factured with.

 md5key_withoutbootloader = DC D7 3A A5 C3 95 98 FB DD F9 E7 F4 0E AE 47 38
 md5key_withbootloader =      8C EF 33 5B D5 C5 CE FA A7 9C 28 DA B2 E9 0F 42

2 - firmware customization and squashfs recompression
We have now enough informations about the firmware header which allows us to grant writing on the device flash.

On the official TP-Link firmware, we have 2 headers, the first at 0x0 and a second one at 0x20200 (in this case). The first section contains the uboot, after the second header kernel + rootfs.

The second header contains the signature made from 0x20200 to EOF with the md5key_withoutbootloader salt
The first md5 signature is made with  md5key_withbootloader from 0x0 to EOF, (thus also including the second image)

As seen in httpd, we have 2 allowed kind of images: the first, is the whole image uboot+kernel+rootfs and the second way is to write just the kernel+rootfs which leaves the uboot uneffected (read: if I fail I can still de-brick by using a serial TTL :) )
That's why I've splitted the firmware.

3 - Firmware file reconstruction
 3.1 Uncompress the image
First of all, from the firmware, we're going to extract the squasfs file and uncompress by using unsquashfs:

Note: binwalk is an amazing swiss-knife, keep in mind the compression xz (LZMA2) and the inodes

By dd tool, squashfs has been extracted skipping, from the firmware file, the first 0x100000 (1048576 in decimal) bytes.
Next step was to uncompress the image with simply with # unsquashfs filename

 3.2 Modify
I've used nano to modify the rcS row number 33
from:
#telnetd -l /bin/login &
to
telnetd -l /bin/login &
Forgot to say: /etc/shadow file contains a different password then the one we use on the web.
Create your new /etc/shadow file!
The TP-Link credential hardcoded are root:shoadmin
(Thank you 6c2e6e2e ) <-wrong password here

(Thank you Openwrt)


3.3 Re-Compress the image
now recompress time with: mksquashfs squashfsdir/ fileout.squashfs -comp xz -no-duplicates
Those last two options are vital. The first indicates to mksquashfs to use LZMA2 algo(the same algo we know the stock firmware is using, showed by binwalk), the second one prevents mksquashfs to delete duplicates, guaranteeing the correct restoration of inodes and file number.

3.4 Put the things togheter 
Anyway the file size is reasonably different different. Anyway we can have a bigger (or smaller) image, anyway not bigger than 0x6C0000 calculated from my reduced (kernel+squashfs) stock firmware (EOF) 0x7C0000 - 0x100000 (initial squashfs magic number).
In the re200_imagecut.bin (obtained in paragraph 2, see image) we overwrite into the file starting from 0x100000 our new squashfs image by keeping the SAME original file size, if needed padding the file adding or removing 0xFF up to 0x7C0000-1




4 - Firmware mod new hash
We have now recreated the right file structure. The last step is to rewrite the new md5 at 0x4c-0x5c.
In my case, bootloaderless, my key will be md5key_withoutbootloader:

By keeping in mind what we read at the paragraph n.2, once replaced the md5 you'll have the new md5 (see the picture at the bottom) wich we will use to replace the salt (in red) from 0x4c to 0x5c.

5 - Upload and verify

Let's upload and try to login with Putty.....

BOOM .... it worked like a charm on the first try!!! 😎


Modified firmware image here.
(no uboot, telnet enabled: default telnet credentials root:sohoadmin)

Cheers,
RE-Solver